[스크랩] [기술통계분석] - 1. 분석의 목적(집중경향치, 분산도)

제 1장. 기술통계 분석

 

 

1. 분석의 목적

 

기술통계 분석은 자료의 특성을 파악하기 위한 목적으로 사용된다. 기술통계 분석을 통해 집중경향치(Central Tendency)와 분산도(Dispersion) 등의 통계치들을 얻을 수 있다.

집중경향치는 점수들이 어떤 값을 중심으로 분포되어 있는지를 나타내며, 분산도는 점수들이 평균으로부터 얼마나 퍼져 있는지를 나타낸다.

기술통계 분석은 등간척도나 비율척도와 같은 연속 변인의 데이터를 분석할 때 사용되는 반면, 빈도분석은 명목척도나 서열척도와 같은 불연속 변인의 데이터를 분석할 때 사용된다.

 

1) 집중경향치

 

집중경향치로는 산술평균(mean; 흔히 평균이라고 한다), 중앙치(Median), 최빈치(Mode)가 있다. 산술평균은 모든 점수를 합한 후, 이를 총 사례수(n)로 나눔으로써 구해지며, 다음과 같이 표기된다:

 

         

 

 

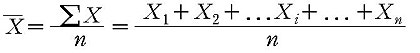
중앙치는 전체 점수 분포의 중앙에 위치된 점수 값(혹은 잠정적 점수 값)을 말한다. 예를 들어, 2, 3, 5, 6, 9로 구성된 점수 집합의 경우 중앙치는 5가 된다. 만약 집합 내 점수의 수가 짝수라면, 중앙치는 중앙의 두 점수의 평균이 된다. 앞에 제시된 집합에 13이 추가되어 5개 대신에 6개의 점수로 집합이 구성되어 있다고 가정해보자. 이 집합의 중앙에 위치된 점수는 5와 6이며, 중앙치는 이 두 점수의 평균인 5.5가 된다.

최빈치는 분포에서 가장 빈도가 높은 값이다. 다음의 자료를 고려해보자:

 

자료: 1, 2, 5, 5, 5, 6, 6, 7, 8

 

위 자료에서 5의 빈도는 3이며, 6의 빈도는 2 그리고 나머지 값들의 빈도는 모두 1이므로 가장 빈도가 높은 5가 최빈치가 된다.

 

 

한걸음 더

 

대표적인 집중경향치로 산술평균을 사용하는 이유

 

연구를 수행함에 있어 특별한 목적을 갖는 경우를 제외하고 대부분의 경우 집중경향치로서 산술평균만을 산출하고, 이를 연구 결과에 제시한다. 이처럼 대표적인 집중경향치로서 산술평균을 사용하는 이유는 산술평균이 세 가지 측정치 가운데 가장 안정적이기 때문이다. 이 때 안정적이라는 말의 의미는 예측의 정확성을 의미한다. 모집단으로부터 일정수의 표본을 추출한 후, 표본을 통해 모집단의 평균을 추정하고자 할 때, 산술평균을 통한 추정의 오차가 중앙치나 최빈치를 통한 추정보다 더 작기 때문에 집중경향치로서 산술평균을 사용한다.

 

 

 

 

   

2) 분산도

 

서로 다른 두 집단의 평균값이 같다고 하여 분포의 모양까지 같은 것은 아니다. 즉, 평균을 중심으로 개별 값들이 모여 있을 수도 있고, 넓게 퍼져 있을 수도 있다. 아래 그림의 a는 평균을 중심으로 개별 값들이 모여 있는 분포의 양상을 보여주는 반면, 그림 b는 개별 값들이 평균을 중심으로 널리 흩어져 있는 분포의 모양을 나타내고 있다. 이처럼 각 개별 값들이 평균을 중심으로 어떻게 분포되어 있는가를 나타내는 것이 분산도(dispersion)이다.

 

 

           

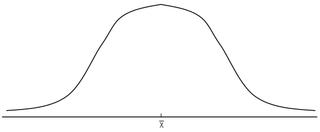
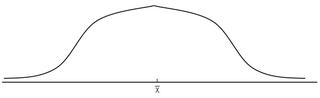
                                         a                                                                                         b

 

분산도에는 범위(range), 변량(variance; 분산이라고도 한다), 표준편차(standard deviation)가 있다. 범위는 최고점수에서 최저점수를 뺀 값(범위 = 최고점수 - 최저점수)을 의미한다. 예를 들어, 2, 6, 8, 11, 15로 구성된 집합의 경우를 가정해보자. 최고점수는 15이고 최저점수는 2임을 알 수 있다. 따라서 범위는 최고점수 15에서 최저점수인 2을 뺀 값인 13이 된다는 것을 알 수 있다.

변량은 각 개별 점수가 평균으로부터 떨어진 정도를 나타내는 편차 점수를 구한 후 이를 제곱하여 모두 더한 다음 구해진 값을 사례수로 나누어줌으로서 구할 수 있다. 각 개별 점수가 평균으로부터 흩어져 있는 정도를 측정하기 위해 각 개별 점수의 편차점수를 모두 구한 다음, 이를 평균하는 방법을 생각해볼 수 있을 것이다. 그러나 이는 현실적으로 불가능하다. 왜냐하면 각 개별 점수들의 편차를 구하면 절반은 양의 편차 점수를 갖고, 절반은 음의 편차 점수를 가져 이를 모두 더하면 0이 되기 때문이다.

이러한 문제점을 해결하기 위해 제곱합을 사용한다. 각 개별 점수의 편차점수를 구한 후, 이를 제곱하여 모두 더한 값을 제곱합(sum of squares: SS)이라고 한다. 제곱합은 다음과 같이 나타내진다:

 

 

 

 

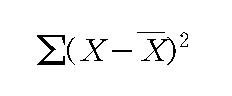
산술평균은 개별 점수의 합을 전체 사례 수(n)로 나누어줌으로써 구할 수 있다는 사실을 살펴보았다. 마찬가지로 평균 분산을 구하기 위해서는 제곱합을 전체 사례 수(n)로 나눠주어야 한다. 평균 분산을 구하기 위해 제곱합을 전체 사례 수로 나누어서 얻어진 값을 변량이라고 한다. 변량의 계산공식은 다음과 같다:

 

 

 

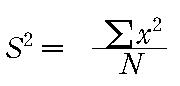
한걸음 더

 

모집단 변량을 추정하는 계산과정에서 자유도를 사용하는 이유?

 

모집단의 변량은 σ²으로 표기하며, 표본 변량은 s²으로 표기한다. 모집단의 표준 편차는 σ로 표기되며, 표본의 표준편차는 s로 표기된다. 변량의 경우처럼, 표준편차의 경우에도 표본의 표준 편차(s)를 통해 모집단 표준편차(σ)를 추정하고자 할 때에는 분모에 자유도가 사용된다.

자료 집합의 특성을 기술하기 위해 변량을 계산하는 경우(전체 집단 구성원의 개별 값을 알고 있는 경우)에는 제곱합을 전체 사례 수로 나누어주면 된다. 그러나 표본 통계치를 통해 모집단의 변량을 추정하고자 할 때에는 제곱합을 자유도인 n-1로 나누어주어야 한다. 자세한 사항은 추후에 다시 논의하기로 하고, 다만 여기서는 자유도로 나누는 것이 표본 자료로부터 모집단 변량(σ²)을 보다 더 정확하게 추정할 수 있기 때문이라는 사실만 이해하기로 하자.

 

 

 

 

 

표준편차는 변량에 제곱근을 함으로써 구해진다. 표준편차는 그 값이 작을수록 개별 값들이 평균 가까이에 분포되어 있음을 의미하며 표준편차의 값이 커질수록 개별 값들이 평균으로부터 멀리 떨어져 분포되어 있음을 나타낸다. 표준편차의 계산 공식은 다음과 같다:

 

 

 

 

 

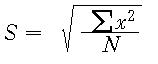
한걸음 더

 

집중경향치와 분산도에 대해 관심을 갖는 이유

 

평균에 대해 관심을 갖는 이유는 예측을 하기 위함이다. 한 학생이 매달 수학 시험을 치렀다고 가정해보자. 이때 그 학생의 수학 점수의 평균이 90점이라는 사실은 그 학생이 향후 시험을 치렀을 때 90점 정도의 점수를 받게 될 것이라는 사실을 예측할 수 있다.

반면, 분산도에 관심을 갖는 이유는 분산도가 주는 두 가지 정보 때문이다. 하나는 예측의 정확성과 관련된다. A학생은 시험을 치를 때마다 점수가 들쭉날쭉하여 분산이 큰 반면, B학생은 점수가 평균 주위에 몰려 있어 분산이 작다고 가정해보자. A학생과 B학생이 새로이 치르는 시험에서 몇 점을 받게 될 것인지를 예측한다고 가정할 때, 예측의 정확성은 어느 쪽이 더 높을 것인가? 당연이 B학생에 대한 예측의 정확성이 더 높게 된다. 즉, 분산이 클수록 평균을 통한 예측의 정확성은 떨어지는 반면 분산이 적을수록 예측의 정확성은 높아진다. 분산도가 제공하는 두 번째 정보는 집단의 동질성에 관한 정보이다. 초등학교 두 개 반이 있다고 가정해보자. 두 개 반 학생들을 대상으로 신장을 측정한 후, 각반의 신장에 대한 분산도를 측정한 결과, A반 학생들의 분산도가 B반 학생들의 분산도보다 더 크다면 우리는 B반 학생들이 A반 학생들보다 더 동질적인 특성(신장이 비슷하다는 사실)을 가지고 있음을 알 수 있다.

 

 

 

 

한걸음 더

 

왜도와 첨도

정규분포는 분포의 형태가 좌우 대칭을 이룬다. 왜도는 분포의 비대칭성 정도 즉, 분포가 기울어진 정도와 방향을 나타낸다. 왜도가 0이면 분포의 형태가 좌우대칭인 정규분포를 뜻하며, 음수이면 부적편포, 양수이면 정적편포를 말한다.

반면, 첨도는 분포의 뾰족한 정도를 의미한다. 분산도가 크면 집단이 이질적이고 분포의 높이가 낮아지며, 분산도가 작으면 집단이 동질적이고 분포의 높이가 높아진다. 정규분포의 첨도는 0이며, 첨도가 0보다 크면 정규분포보다 더 뾰족한 모양을 갖는데, 이를 급첨(leptokurtic)이라 하고, 첨도가 0보다 작으면 분포의 높이가 정규분포보다 낮아지는데, 이를 평성(platykurtic)이라 한다.